Ignacio Sepúlveda
SDSU Coastal Engineering
Tsunami models: Relevant Studies
The largest tsunamis are often attributed to earthquakes in subduction zones. This has led my career to study the physics of earthquakes and their tsunamigenic potential. Recently, we have also investigated other tsunamigenic processes, such as landslides and volcanic eruptions. Our understanding of tsunamis and other coastal hazards has a high societal impact. Nearly 40% of the world population live within 100 miles from the coast. Thus, tsunamis and other coastal hazards can significantly impact the life of the inhabitants of a country and their economy. Here I explain some of my work on tsunami and earthquake models.
Volcanic tsunamis
The 2022 Tonga tsunami was an interesting event, with significant impacts all around the world. The most interesting aspect was the global tsunami that reached all the oceans and which was generated by an acoustic air wave produced by the volcanic eruption. The volcanic tsunamigenic mechanism can be classified in two. One is the classic mechanism related to caldera/flank collapses and the other is related to the air wave generation. In the animation at the right, you can see the tsunamigenic air wave mechanism. Note that the air wave can actually produce two waves: couple and uncouples tsunami waves!.


The model validation went so well that we wanted to test the model with another tsunamigenic volcanic eruption: The 1883 Krakatoa eruption. Using meteorological model data reconstructing atmospheric processes of August 1883 and description of the air wave (from the Royal Society), we simulated and validated our model. Similarities are amazingly close (see below). Future work are to better simulate local tsunamis within bays for the 2022 and 1883 volcanic tsunamis.
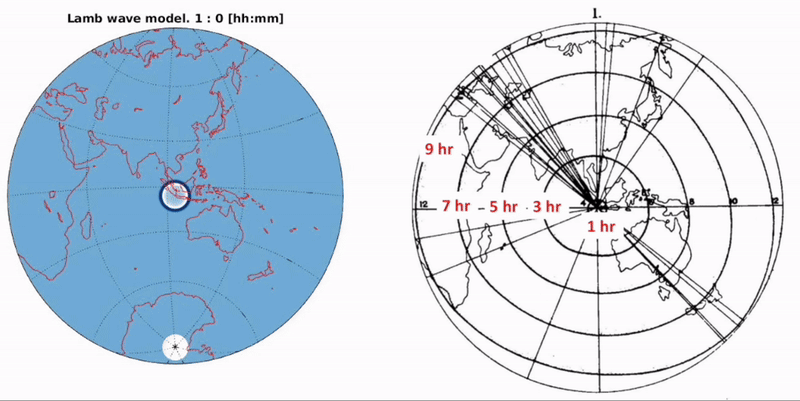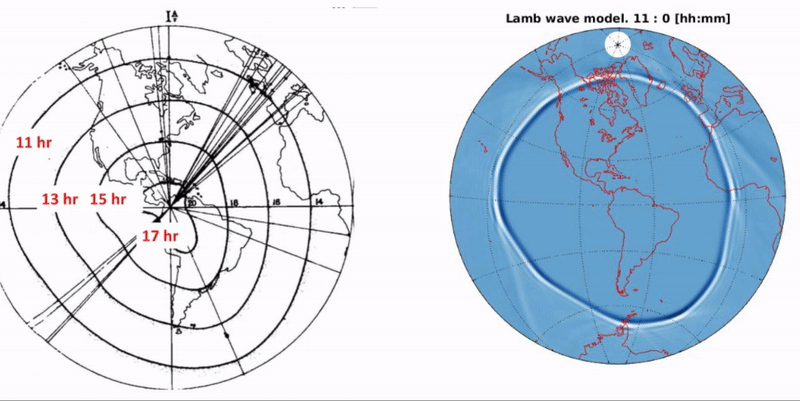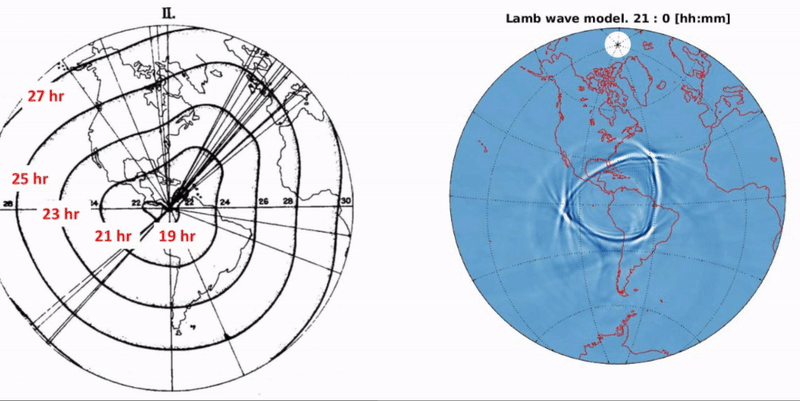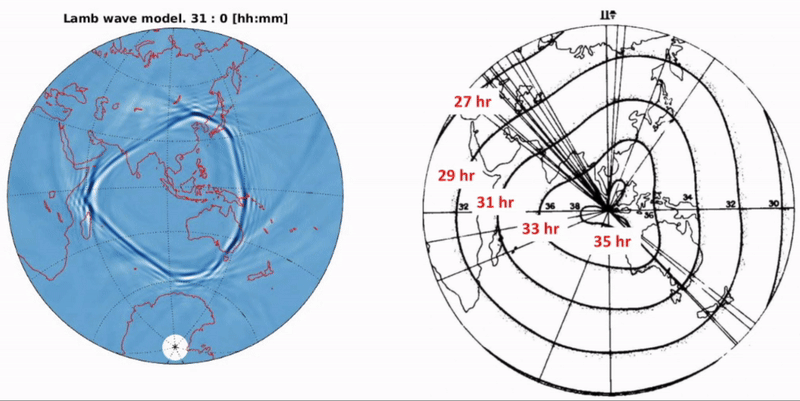
When analyzing the atmospheric pressure disturbances, we discovered that arrival times and amplitudes were significantly asymmetric. Two possible reasons where the topography and global winds. To test these potential contributions, we derived a new governing equation which was implemented in a numerical model. When comparing the model (called Augmented Model) with satellites images of the air wave, we observed a great agreement that is much better than the classic and standard types of air wave models (see animation at the left and video).
The 2022 Tonga tsunami prompted the development of a new COMCOT tsunami model code. This new code is meant to be used in hazard and risk assessments. The code includes the simulation of the air acoustic-wave generated during explosive eruptions. This air wave produces tsunamis via pressure changes. The equations are solved solved using two-way coupled nesting grids. The new code was validated using re-analysis data of surface atmospheric pressure and measurements of sea levels at tide gauge stations. The model shows very satisfactory results. The traditional volcanic tsunami mechanisms such as caldera/flank collapses are included in the original code of COMCOT and can be combined with the air wave, fully modeling volcanic tsunami sources.

Meteo-tsunamis
Storms produce storm surge due to forces related to the atmospheric pressure and strong winds. Sometimes the size and time scales of these forces are special enough to create long waves propagating with important amplitudes in coastal regions. These waves are called meteo-tsunamis.
Estimating tsunami runup with earthquake fault plane parameters
With my PhD advisor, Dr. Philip Liu, we proposed closed-form expression to estimate the runup of tsunami waves, in terms of the characteristics of the earthquake that generates it. The closed-form expressions can be used for tsunami early-warning in the case that earthquake fault parameters are known. We also proposed closed form expression for a breaking criterion. Paper published in Journal of Coastal Engineering.
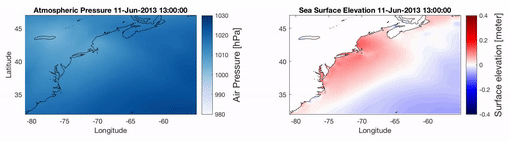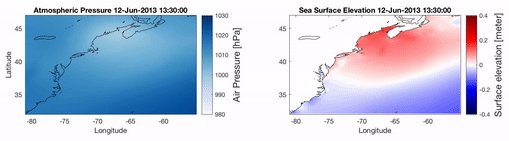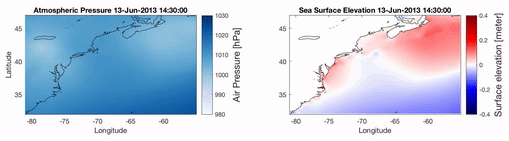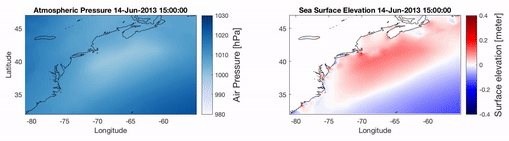
A new code based on COMCOT is under development to simulate metro-tsunamis. The video shows a preliminary simulation of a metro-tsunamis produced in 2013 in the US East coast.

Left: Runup, R, is related with the earthquake slip (s), the earthquake depth (d), the fault width (W), the distance of the earthquake (ld) and the dip angle (delta). This solution is derived for a initial valued problem of tsunami, which is generated over a sloping beach. Other solutions are derived for a boundary value problem. We also derived a breaking criterion, as the solutions consider non-breaking waves. Right: Two analytical solutions are derived for two different coastal geometries. The composite slope problem is solved with a boundary-value problem. The constant slope problem is solved with an initial-valued problem.


Review of seismic/tsunami waves generation models
Tsunami hazard assessments are not only uncertain due to the input data, but also because of the simplifications of our earthquake and tsunami models. Tsunami models can be divided in generation and propagation models. While the tsunami propagation models have experienced significant improvements in the recent decades (e.g. considering frequency dispersion, non linearity and more complex. model in the breaking zone), the tsunami generation models have had a small evolution. In this research, we aim review the state of the art in tsunami generation models. We are focusing our study on shallow earthquakes. We are employing the tsunami model COMCOT and the seismic wave model F-K.

Left: Because tsunamis are sensitive to earthquake properties, we need to understand the tsunami-earthquake interaction in a better way. A very relevant problem are the case of shallow earthquakes. We extended our work to recognize if seismic waves can capture differences in the earthquake properties. We performed preliminar sensitivity analyses of seismic waves close to the source, as a function of the statistics properties of synthetic earthquakes. This exercise aims to identify if seismic waves are sensitive to properties of the rupture (e.g. slip distribution properties, such as spectral decay H). If that is the case, then we would be able to identify relevant properties from seismic wave records of shallow earthquakes. The simulations are made using F-K model. The curves show the power spectral densities of seismic waves in a close station to the source. Our analyses shows that seismic waves are not sensitive to the number of kl terms and the decay parameter H. However, the rupture velocity can produce some effects on seismic waves. Segmented lines show a -1 and -2 power decay law. Right: Preliminar sensitivity analysis of tsunami waves in the far (Hong Kong) and near field (Kao Hsiung) to the source (i.e. earthquakes in the Manila subduction zone), as a function of the statistical properties of earthquake slip distribution.


We conducted a tsunami source inversion for the 2014 Iquique Chile tsunami using the classic shallow wave theory and a linear wave model considering dispersion (e.g. Kajiura model). Top-left panel shows the inverted earthquake slip distribution using linear wave modeling for the Green functions generation and tsunami wave records from DART buoys. The bottom-left panel show the tsunami initial surface elevation which defines the "starting point" of the tsunami propagation. The top-right panel shows the differences of the inversion using shallow wave theory and linear wave modeling (with dispersion). The bottom-right panel shows the differences on the inverted tsunami initial surface elevations. The linear wave model predicts that high wavenumber content of the initial condition is absent.
We are also studying the modeling of the tsunami initial condition for shallow earthquakes, in which some common simplifications may not be longer valid. We are assessing the impact of near-source dispersion effects, the effects of earth's crustal heterogeneity and seafloor topography on co-seismic deformations and the effect of seafloor horizontal deformations.
Tsunami-tide interaction simulated with non-linear shallow water wave equations
In this study we combined tides and tsunamis in a non-linear shallow water wave equations model using the suite Mike21 Flow Model FM. The methodology first requires the construction of a validated regional tidal model. The methodology was applied for a study case in Chacao Channel, Chile, and the 1960 earthquake. Tsunami+tide surface elevation and flows were assessed in Roca Remolinos (at the center of the channel). A paper was published in JGR Oceans.

Left: View of Chacao Channel and Roca Remolinos. Right: Validation of tidal model in Roca Remolinos by comparing our simulation (dots) with records (lines) of tidal elevation and current speed. Correlations of elevation and current speeds yield 90% and 72%, respectively. Bottom: Tsunami elevations by considering different tides. Changes in the tsunami response are significant.


Coastal impacts
Tsunami disasters occur when the infrastructure systems reach a level of failure. Tsunami hazard assessments are combined with fragility analyses to quantify the real vulnerability to tsunamis. We have studied of the effect of tsunamis in coastal facilities and have proposed solutions to reduce the chances of disasters.
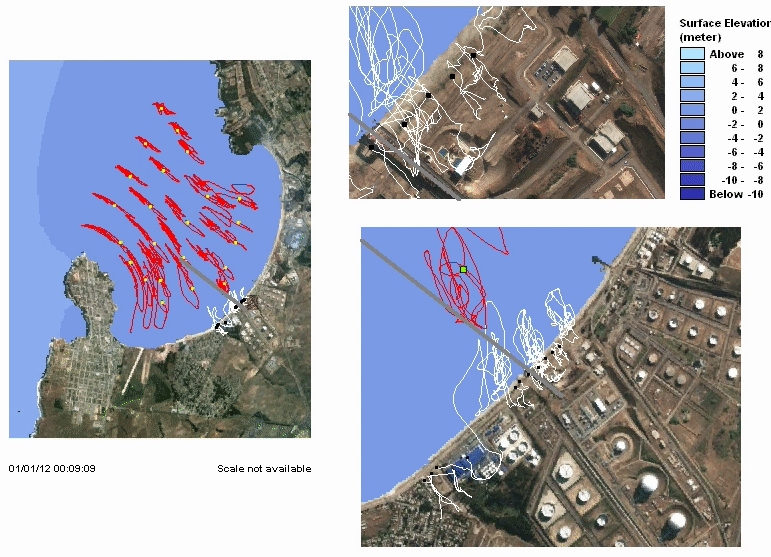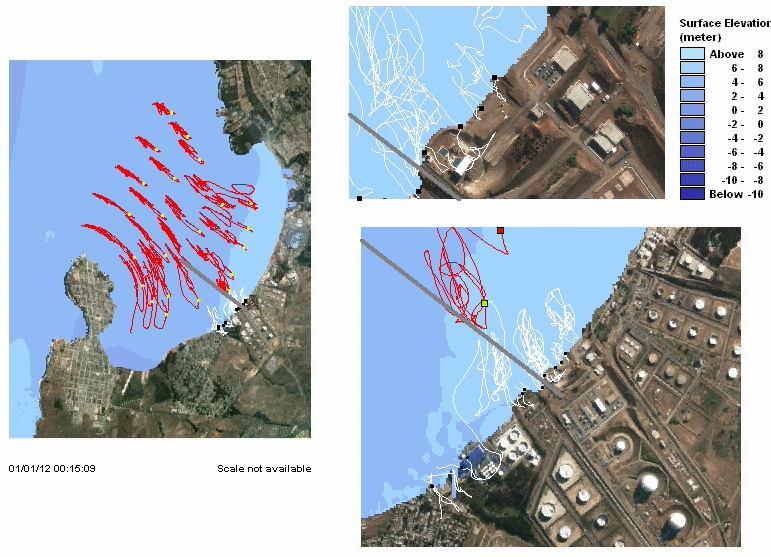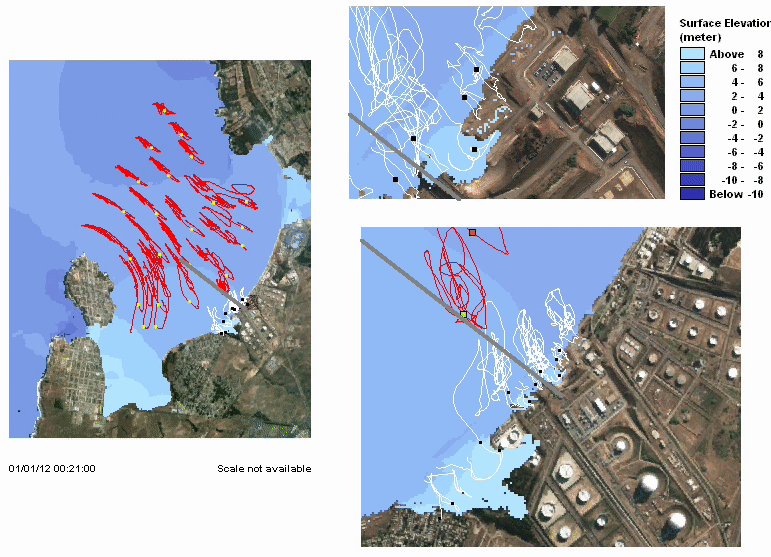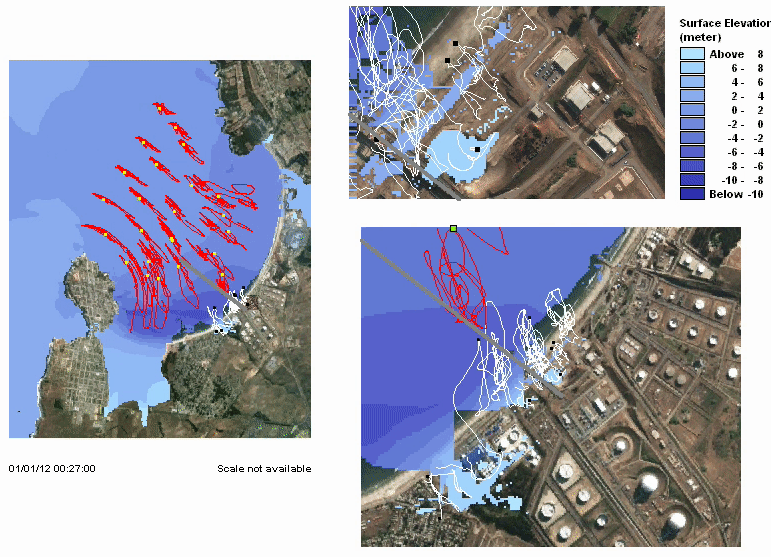
Studying past events
It is essential to study past event to improve earthquake and tsunami models. I have participated on the study of some recent events. I am also interested on other coastal hazards (e.g. meteotsunamis). Here I include some publications:
Carvajal, M., Contreras-López, M., Winckler, P., & Sepúlveda, I. (2017). Meteotsunamis occurring along the southwest coast of South America during an intense storm. Pure Appl. Geophys., 174 (2017), 3313–3323. DOI:10.1007/s00024-017-1584-0
Contreras-López, M., Winckler, P., Sepúlveda, I., Andaur-Álvarez, A., Cortés-Molina, F., Guerrero, C. J. & Vergara, H. (2016). Field survey of the 2015 Chile tsunami with emphasis on coastal wetland and conservation areas. Pure and Applied Geophysics, 173.2 (2016), 349–367. DOI:10.1007/s00024-015-1235-2.
An, C., Sepúlveda, I., Liu, P. (2014). Tsunami source and its validation of the 2014 Iquique, Chile, earthquake.Geophysical Research Letters. Volume 41 Issue 11. Pages 3988–3994. DOI: 10.1002/2014GL060567.